Dalam dunia matematika, khususnya statistika, istilah median mungkin sudah tidak asing lagi bagi Anda. Median adalah nilai tengah dari sekumpulan data yang telah diurutkan. Namun, bagaimana jika kita ingin membagi data menjadi empat bagian yang sama besar? Di sinilah konsep kuartil berperan. Jika Anda belum familiar dengan kuartil, artikel ini akan membantu Anda memahami pengertian kuartil, jenis-jenisnya, serta cara menghitungnya untuk data tunggal dan berkelompok. Mari kita pelajari lebih dalam!
Pengertian Kuartil
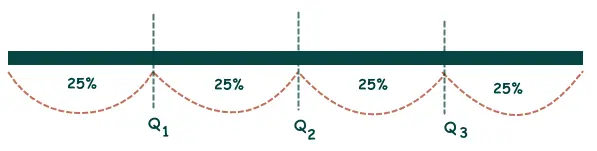
Kuartil adalah nilai-nilai yang membagi sekumpulan data terurut menjadi empat bagian sama besar, di mana setiap bagian mewakili 25% dari total data. Kuartil adalah alat statistik yang digunakan untuk mengetahui distribusi data dengan membaginya menjadi empat bagian yang sama besar. Kuartil membantu kita memahami bagaimana data tersebar dan di mana letak konsentrasinya.
Dalam kuartil, terdapat tiga titik pembagi utama, yaitu:
- Kuartil Pertama (Q1): Memisahkan 25% data terendah dari 75% data lainnya.
- Kuartil Kedua (Q2): Sama dengan median, memisahkan 50% data terendah dan 50% data tertinggi.
- Kuartil Ketiga (Q3): Memisahkan 75% data terendah dari 25% data tertinggi.
Kuartil dalam Data Tunggal
Data tunggal adalah data yang disajikan dalam bentuk satu per satu, tidak dikelompokkan dalam interval kelas. Contohnya adalah daftar nilai ujian siswa, tinggi badan individu, atau berat barang.
Untuk menghitung kuartil dalam data tunggal, langkah-langkahnya adalah:
- Mengurutkan Data: Susun data dari nilai terkecil hingga terbesar.
- Menentukan Letak Kuartil: Gunakan rumus untuk mencari posisi kuartil dalam data.
- Menentukan Nilai Kuartil: Ambil nilai data pada posisi yang telah ditentukan.
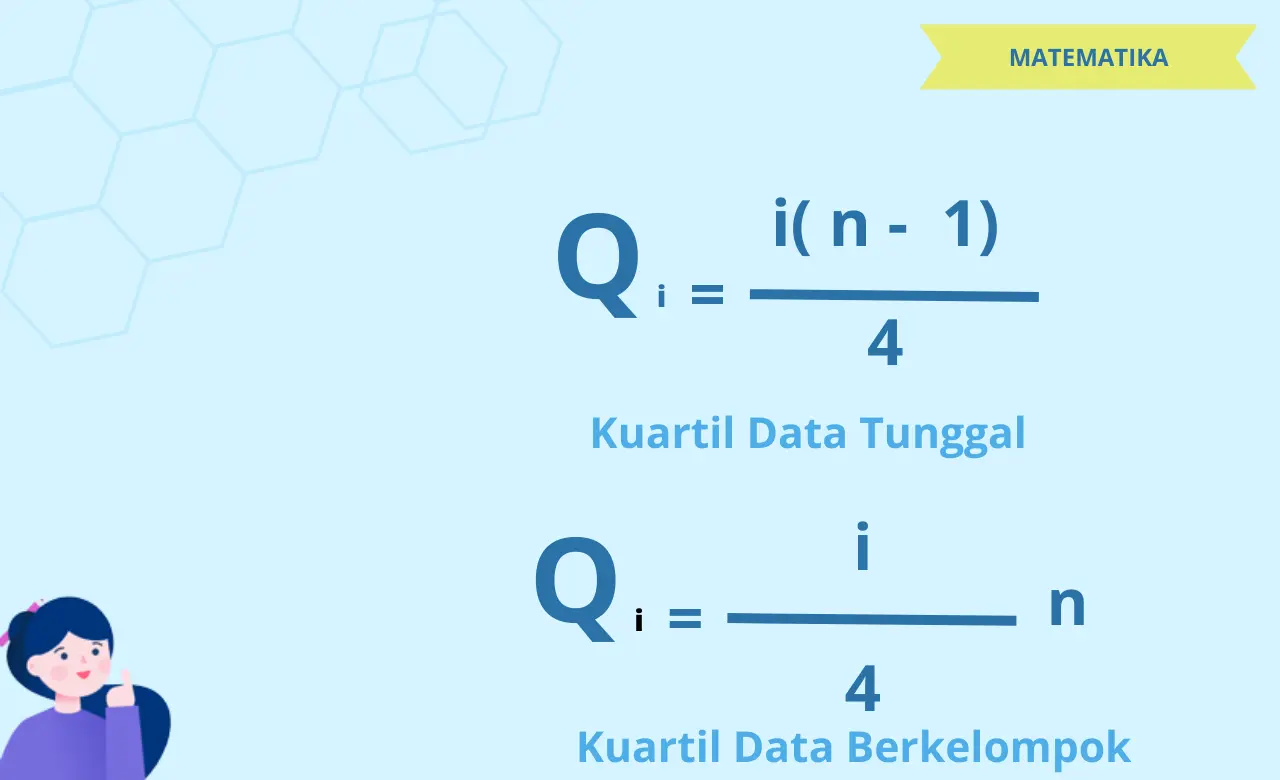
Rumus Letak Kuartil Data Tunggal
Untuk menentukan letak kuartil ke-i (Qi) dalam data tunggal, gunakan rumus:
LQi = (i × (n + 1)) / 4
Dengan:
- LQi: Letak kuartil ke-i
- i: Nomor kuartil (1, 2, atau 3)
- n: Jumlah total data
Contoh Menghitung Kuartil Data Tunggal
Contoh 1:
Diberikan data nilai ujian berikut:
8, 7, 6, 9, 5, 7, 8, 6, 5, 9
Langkah 1: Urutkan data:
5, 5, 6, 6, 7, 7, 8, 8, 9, 9
Langkah 2: Tentukan jumlah data:
n = 10
Langkah 3: Cari letak Q1:
LQ1 = (1 × (10 + 1)) / 4 = 2.75
Posisi 2.75 berarti kita perlu mengambil rata-rata antara data ke-2 dan ke-3.
Data ke-2: 5
Data ke-3: 6
Nilai Q1:
Q1 = 5 + (0.75 × (6 - 5)) = 5 + 0.75 = 5.75
Langkah 4: Cari letak Q2 (Median):
LQ2 = (2 × (10 + 1)) / 4 = 5.5
Posisi 5.5 berarti rata-rata antara data ke-5 dan ke-6.
Data ke-5: 7
Data ke-6: 7
Nilai Q2:
Q2 = 7
Langkah 5: Cari letak Q3:
LQ3 = (3 × (10 + 1)) / 4 = 8.25
Posisi 8.25 berarti kita perlu mengambil rata-rata antara data ke-8 dan ke-9.
Data ke-8: 8
Data ke-9: 9
Nilai Q3:
Q3 = 8 + (0.25 × (9 - 8)) = 8 + 0.25 = 8.25
Hasil:
- Q1 = 5.75
- Q2 = 7
- Q3 = 8.25
Kuartil dalam Data Berkelompok
Data berkelompok adalah data yang disajikan dalam bentuk interval kelas. Contohnya adalah distribusi frekuensi tinggi badan siswa dalam rentang tertentu.
Untuk menghitung kuartil dalam data berkelompok, kita perlu menggunakan rumus yang mempertimbangkan frekuensi dan interval kelas.
Rumus Kuartil Data Berkelompok
Qi = L + [(i × n / 4) - F] / f × p
Dengan:
- Qi: Kuartil ke-i
- L: Tepi bawah kelas kuartil ke-i
- i: Nomor kuartil (1, 2, atau 3)
- n: Jumlah total data
- F: Frekuensi kumulatif sebelum kelas kuartil
- f: Frekuensi kelas kuartil
- p: Panjang interval kelas
Contoh Menghitung Kuartil Data Berkelompok
Contoh 2:
Diberikan data distribusi nilai ujian siswa:
| Nilai | Frekuensi |
|---|---|
| 40-49 | 5 |
| 50-59 | 8 |
| 60-69 | 12 |
| 70-79 | 10 |
| 80-89 | 5 |
Langkah 1: Hitung jumlah data (n):
n = 40
Langkah 2: Hitung frekuensi kumulatif:
- Frekuensi kumulatif: 5, 13, 25, 35, 40
Langkah 3: Tentukan posisi Q1:
Posisi Q1 = (1 × 40) / 4 = 10
Langkah 4: Tentukan kelas Q1:
Posisi ke-10 terdapat pada kelas 50-59.
Langkah 5: Tentukan nilai yang diperlukan:
- L (tepi bawah kelas) = 50 – 0,5 = 49,5
- F (frekuensi kumulatif sebelum kelas Q1) = 5
- f (frekuensi kelas Q1) = 8
- p (panjang interval kelas) = 10
Langkah 6: Hitung Q1:
Q1 = 49,5 + [(10 - 5) / 8] × 10 = 49,5 + (5 / 8) × 10 = 49,5 + 6,25 = 55,75
Hasil:
Q1 = 55,75
Contoh Soal dan Pembahasan Lainnya
Contoh 3
Diberikan data tinggi badan 30 siswa sebagai berikut:
| Tinggi Badan (cm) | Frekuensi |
|---|---|
| 150-154 | 4 |
| 155-159 | 6 |
| 160-164 | 10 |
| 165-169 | 7 |
| 170-174 | 3 |
Tentukan kuartil ke-2 (Median) dari data tersebut.
Pembahasan:
Langkah 1: Hitung jumlah data (n):
n = 30
Langkah 2: Hitung frekuensi kumulatif:
- Frekuensi kumulatif: 4, 10, 20, 27, 30
Langkah 3: Tentukan posisi Q2:
Posisi Q2 = (2 × 30) / 4 = 15
Langkah 4: Tentukan kelas Median:
Posisi ke-15 terdapat pada frekuensi kumulatif 20, yaitu kelas 160-164.
Langkah 5: Tentukan nilai yang diperlukan:
- L (tepi bawah kelas) = 160 – 0,5 = 159,5
- F (frekuensi kumulatif sebelum kelas Median) = 10
- f (frekuensi kelas Median) = 10
- p (panjang interval kelas) = 5
Langkah 6: Hitung Median:
Median = 159,5 + [(15 - 10) / 10] × 5 = 159,5 + (5 / 10) × 5 = 159,5 + 2,5 = 162
Hasil: Median (Q2) = 162 cm
Contoh 4
Diberikan data penghasilan bulanan (dalam juta rupiah) dari 50 karyawan sebagai berikut:
| Penghasilan (juta Rp) | Frekuensi |
|---|---|
| 2 – 4 | 5 |
| 5 – 7 | 15 |
| 8 – 10 | 20 |
| 11 – 13 | 7 |
| 14 – 16 | 3 |
Tentukan kuartil ke-3 dari data tersebut.
Pembahasan:
Langkah 1: Hitung jumlah data (n):
n = 50
Langkah 2: Hitung frekuensi kumulatif:
- Frekuensi kumulatif: 5, 20, 40, 47, 50
Langkah 3: Tentukan posisi Q3:
Posisi Q3 = (3 × 50) / 4 = 37,5
Langkah 4: Tentukan kelas Q3:
Posisi ke-37,5 terdapat pada frekuensi kumulatif 40, yaitu kelas 8 – 10.
Langkah 5: Tentukan nilai yang diperlukan:
- L (tepi bawah kelas) = 8 – 0,5 = 7,5
- F (frekuensi kumulatif sebelum kelas Q3) = 20
- f (frekuensi kelas Q3) = 20
- p (panjang interval kelas) = 3
Langkah 6: Hitung Q3:
Q3 = 7,5 + [(37,5 - 20) / 20] × 3 = 7,5 + (17,5 / 20) × 3 = 7,5 + 2,625 = 10,125
Hasil: Q3 = 10,125 juta rupiah
Penggunaan Kuartil dalam Dunia Bisnis dan Statistik
Kuartil tidak hanya digunakan dalam bidang pendidikan, tetapi juga di berbagai industri, terutama dalam analisis bisnis dan statistik. Berikut beberapa contoh penerapan kuartil dalam kehidupan nyata:
- E-commerce: Kuartil digunakan untuk membagi penjual ke dalam kelompok-kelompok berdasarkan kinerja mereka, seperti 25% penjual terbaik, penjual dengan rating tertinggi, atau pendapatan terbesar. Ini membantu perusahaan untuk memfokuskan upaya pemasaran pada segmen-segmen tertentu.
- Analisis Keuangan: Dalam industri keuangan, kuartil digunakan untuk membagi portofolio investasi berdasarkan kinerja. Misalnya, 25% aset terbaik, aset dengan return tertinggi, atau aset paling berisiko.
- Penelitian Kesehatan: Di bidang kesehatan, kuartil dapat digunakan untuk menganalisis distribusi data pasien berdasarkan variabel-variabel seperti usia, berat badan, atau hasil tes laboratorium. Hal ini berguna untuk mengidentifikasi pasien yang termasuk dalam 25% dengan risiko tertinggi.
- Pengukuran Produktivitas: Kuartil dapat digunakan untuk mengelompokkan karyawan berdasarkan kinerja atau produktivitas, sehingga manajemen dapat memberikan penghargaan kepada 25% karyawan dengan kinerja terbaik atau memberikan pelatihan tambahan untuk 25% dengan kinerja terendah.
Pentingnya Memahami Kuartil dalam Analisis Data
Menguasai konsep kuartil sangat penting bagi siapa saja yang bekerja dengan data. Berikut alasan mengapa pemahaman kuartil sangat bermanfaat dalam analisis data:
- Distribusi Data: Kuartil membantu untuk memahami bagaimana data tersebar, apakah ada kecenderungan atau ketimpangan dalam data. Ini penting dalam membuat keputusan yang berdasarkan pada distribusi data.
- Identifikasi Outlier: Kuartil memungkinkan kita untuk mengidentifikasi outlier atau data yang menyimpang dari pola umum. Dengan mendeteksi outlier, kita dapat menganalisis lebih dalam tentang anomali tersebut.
- Pembagian Data Secara Adil: Dalam bisnis dan keuangan, kuartil memungkinkan kita membagi data menjadi kelompok-kelompok yang lebih mudah dianalisis. Misalnya, perusahaan dapat menggunakan kuartil untuk membagi pelanggan berdasarkan nilai transaksi mereka.
- Pengambilan Keputusan Berbasis Data: Dengan memahami kuartil, pengambilan keputusan dapat dilakukan berdasarkan data yang tersegmentasi. Ini membantu dalam memberikan fokus pada kelompok tertentu, misalnya, pada 25% pelanggan yang paling menguntungkan.
Kuartil sebagai Alat Pengukuran yang Efektif
Kuartil adalah alat yang sangat berguna untuk membagi dan menganalisis data dalam berbagai konteks. Penggunaannya tidak terbatas pada bidang akademik saja, melainkan telah berkembang di berbagai industri seperti bisnis, keuangan, kesehatan, dan penelitian. Pemahaman yang kuat tentang kuartil dapat membantu para profesional dalam mengelola data secara lebih efektif dan membuat keputusan yang lebih terinformasi.
Dengan menggunakan kuartil, kita dapat mengelompokkan data menjadi empat bagian yang sama besar, yang memudahkan analisis dan interpretasi. Dalam dunia bisnis, misalnya, analisis kuartil membantu untuk mengidentifikasi kelompok pelanggan, karyawan, atau penjual berdasarkan performa atau metrik lainnya. Hal ini memungkinkan perusahaan untuk memfokuskan sumber daya pada segmen-segmen yang paling menguntungkan.
Latihan dan Praktik Menghitung Kuartil
Untuk menguasai konsep kuartil, latihan adalah kunci. Berikut adalah beberapa langkah yang bisa Anda lakukan untuk melatih pemahaman tentang kuartil:
- Kumpulkan Data: Mulailah dengan data sederhana, seperti nilai ujian atau hasil penjualan. Urutkan data dari yang terkecil hingga terbesar.
- Tentukan Letak Kuartil: Gunakan rumus yang sudah dijelaskan di atas untuk menentukan posisi kuartil ke-1, ke-2, dan ke-3.
- Bandingkan Hasil: Setelah menemukan nilai kuartil, cobalah untuk menganalisis data berdasarkan kuartil yang telah dihitung. Apa yang bisa Anda simpulkan dari pembagian data tersebut?
- Cobalah dengan Data Berkelompok: Jika sudah paham dengan data tunggal, lanjutkan dengan latihan menggunakan data berkelompok yang melibatkan interval kelas dan frekuensi.