topreneur.id – Pernahkah kamu bercermin sebelum berangkat sekolah? Saat melihat bayanganmu di cermin, kamu mungkin tidak menyadari bahwa yang terjadi adalah peristiwa refleksi atau pemantulan. Menariknya, jarak antara dirimu dengan cermin selalu sama dengan jarak bayanganmu ke cermin. Coba saja menjauhkan diri dari cermin, pasti bayanganmu juga akan mengecil. Nah, dalam Matematika, peristiwa ini merupakan salah satu contoh transformasi geometri. Jadi, apa itu sebenarnya transformasi geometri? Yuk, kita bahas lebih lanjut!
Pengertian Transformasi Geometri
Transformasi secara sederhana berarti perubahan, dan geometri adalah bidang matematika yang mempelajari bangun, garis, titik, dan ukurannya. Transformasi geometri adalah perubahan posisi dan ukuran suatu objek dalam bidang geometri, seperti garis, titik, atau kurva. Dengan kata lain, transformasi geometri mempengaruhi bentuk atau posisi objek tersebut.
Dalam kehidupan sehari-hari, contohnya adalah saat kita melihat bayangan di cermin atau ketika memindahkan benda dari satu tempat ke tempat lain. Transformasi ini dapat digambarkan menggunakan koordinat Cartesius atau matriks.
Jenis-Jenis Transformasi Geometri
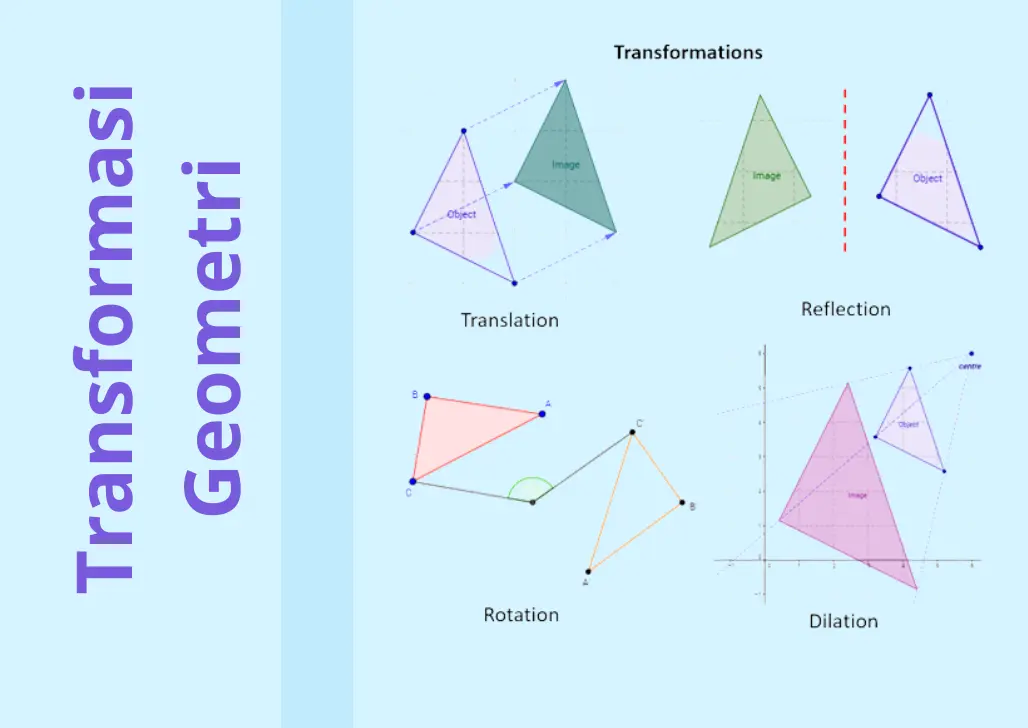
Ada empat jenis transformasi geometri yang umum dijumpai: translasi, refleksi, rotasi, dan dilatasi. Mari kita bahas satu per satu!
1. Translasi
Translasi adalah perpindahan posisi suatu objek tanpa mengubah ukuran atau bentuknya. Jika dijelaskan menggunakan koordinat Cartesius, translasi adalah perpindahan titik-titik koordinat objek ke arah tertentu dengan jarak yang telah ditentukan. Misalnya, kamu memindahkan sebuah bangun dari satu titik ke titik lainnya.
Rumus translasi dapat dinyatakan sebagai:
P’(x’, y’) = P(x + a, y + b)
- P(x, y) = koordinat awal objek.
- a = pergeseran sepanjang sumbu-x.
- b = pergeseran sepanjang sumbu-y.
Contoh: Jika suatu persegi bergeser 5 satuan ke kanan (positif) dan 5 satuan ke bawah (negatif), maka translasi tersebut dapat dihitung menggunakan koordinat awal tiap sudut persegi.
2. Refleksi
Refleksi atau pencerminan adalah perpindahan suatu objek melalui cermin, menghasilkan bayangan yang terbalik. Sama seperti di cermin, jarak antara objek asli dan cermin sama dengan jarak bayangannya.
Refleksi bisa terjadi terhadap sumbu-x, sumbu-y, atau garis tertentu seperti y = x. Berikut adalah rumus refleksi:
- Refleksi terhadap sumbu-x: P’(x, -y)
- Refleksi terhadap sumbu-y: P’(-x, y)
3. Rotasi
Rotasi adalah perputaran suatu objek di sekitar titik tertentu dengan sudut tertentu. Misalnya, memutar sebuah objek searah atau berlawanan dengan arah jarum jam. Rotasi dapat dilakukan terhadap titik pusat (0, 0) atau titik lain sebagai pusat putaran.
Rumus rotasi terhadap titik pusat (0,0) sejauh sudut α adalah:
P’(x’, y’) = R(P, α)
Misalnya, memutar titik M(4, -2) sejauh 90° berlawanan dengan jarum jam akan menghasilkan titik baru M’(2, 4).
4. Dilatasi
Dilatasi adalah transformasi yang memperbesar atau memperkecil ukuran suatu objek berdasarkan faktor pengali tertentu (k). Dilatasi dapat mengubah ukuran objek, tetapi tidak mengubah bentuknya.
- Jika k > 1, objek akan diperbesar.
- Jika 0 < k < 1, objek akan diperkecil.
Contoh: Jika suatu persegi diperbesar dengan faktor pengali k = 2, maka ukuran persegi tersebut akan menjadi dua kali lipat.
Contoh Soal Transformasi Geometri
Contoh Soal 1: Refleksi
Titik G(2, 5) direfleksikan terhadap garis y = -x. Tentukan bayangan titik G!
Pembahasan: Koordinat bayangan G dapat dihitung menggunakan rumus refleksi terhadap garis y = -x, yaitu P’(-y, -x). Sehingga bayangan titik G adalah G’(-5, -2).
Contoh Soal 2: Rotasi
Titik H(1, 3) dirotasi sejauh 180° terhadap titik pusat (0, 0). Tentukan koordinat bayangannya!
Pembahasan: Dengan menggunakan rumus rotasi sejauh 180°, diperoleh koordinat H’(-1, -3).
Contoh Soal 3: Dilatasi
Titik B(2, -1) didilatasi terhadap pusat (4, 2) dengan faktor pengali 2. Tentukan koordinat bayangan titik B!
Pembahasan: Koordinat bayangan B’ dapat dihitung menggunakan rumus dilatasi. Diperoleh B’(0, -4).
Transformasi geometri tidak hanya penting dalam Matematika tetapi juga memiliki banyak aplikasi dalam kehidupan sehari-hari. Dari translasi hingga refleksi, transformasi ini membantu kita memahami perubahan posisi dan ukuran suatu objek dalam berbagai situasi. Dengan menguasai konsep-konsep ini, kamu bisa lebih mudah menyelesaikan soal-soal geometri dan mengaplikasikannya dalam kehidupan nyata.
Semoga penjelasan ini dapat membantu kamu memahami transformasi geometri dengan lebih baik. Selamat belajar!
Tips Penting untuk Menyelesaikan Soal Transformasi Geometri
Menyelesaikan soal transformasi geometri bisa menjadi tantangan, terutama jika kamu baru mempelajarinya. Berikut adalah beberapa tips yang bisa membantu kamu lebih mudah memahami dan menyelesaikan soal-soal transformasi geometri:
- Pelajari Rumus Dasar: Pastikan kamu sudah menguasai rumus dasar untuk setiap jenis transformasi, seperti translasi, refleksi, rotasi, dan dilatasi. Setiap jenis transformasi memiliki rumus dan aturan yang berbeda, jadi penting untuk menguasainya terlebih dahulu.
- Perhatikan Tanda Koordinat: Saat melakukan refleksi atau rotasi, pastikan kamu memperhatikan perubahan tanda koordinat, terutama ketika hasil bayangan terletak pada kuadran yang berbeda di bidang Cartesius.
- Gunakan Diagram: Gambar diagram atau koordinat Cartesius bisa sangat membantu untuk memvisualisasikan transformasi yang sedang kamu kerjakan. Ini juga bisa membantu memeriksa apakah hasil akhir transformasi sudah sesuai dengan ekspektasi.
- Praktekkan Soal-Soal Beragam: Semakin sering kamu berlatih soal-soal transformasi geometri, semakin cepat kamu memahami konsepnya. Cobalah soal dengan berbagai variasi, seperti translasi di arah berbeda atau rotasi dengan sudut yang beragam.
- Jangan Lupa Faktor Pengali dalam Dilatasi: Saat mengerjakan soal dilatasi, perhatikan faktor pengalinya. Dilatasi akan mengubah ukuran objek tergantung dari faktor pengali tersebut, baik memperbesar atau memperkecil.
Kesalahan Umum dalam Transformasi Geometri
Berikut adalah beberapa kesalahan umum yang sering terjadi saat menyelesaikan soal transformasi geometri. Perhatikan ini agar kamu bisa menghindarinya:
- Salah Memahami Arah Translasi: Sering kali, siswa bingung tentang arah pergeseran translasi, terutama ketika bergerak ke arah negatif di sumbu-x atau sumbu-y. Pastikan kamu memahami arah pergeseran dengan benar sebelum menghitung.
- Keliru dalam Rotasi: Kesalahan umum dalam rotasi adalah salah menandai sudut rotasi, apakah searah jarum jam atau berlawanan. Ingat, rotasi searah jarum jam menghasilkan sudut negatif, sementara yang berlawanan positif.
- Lupa Memperhatikan Faktor Pengali: Dalam soal dilatasi, sering kali siswa lupa memasukkan faktor pengali yang mengubah ukuran objek. Akibatnya, bayangan objek tidak sesuai dengan hasil yang benar.
- Tidak Menggunakan Matriks Saat Dibutuhkan: Matriks adalah cara yang sangat berguna untuk menghitung hasil transformasi geometri, terutama untuk soal yang melibatkan rotasi atau refleksi. Jangan lupa menggunakan metode matriks jika diperlukan.
Latihan Tambahan untuk Transformasi Geometri
Agar pemahamanmu semakin mantap, berikut ini beberapa soal latihan tambahan yang bisa kamu coba:
Latihan 1: Translasi
Diketahui titik P(3, 4). Jika titik tersebut ditranslasikan sejauh 5 satuan ke kiri dan 2 satuan ke bawah, tentukan koordinat akhir titik P!
Latihan 2: Refleksi
Titik A(4, -3) direfleksikan terhadap sumbu-x. Tentukan koordinat bayangan titik A!
Latihan 3: Rotasi
Rotasikan titik B(-2, 3) sejauh 90° berlawanan dengan arah jarum jam terhadap titik pusat (0,0). Tentukan koordinat titik bayangan B!
Latihan 4: Dilatasi
Sebuah segitiga ABC dengan koordinat A(1, 2), B(3, 4), dan C(5, 6) didilatasi terhadap titik pusat (0, 0) dengan faktor pengali 2. Tentukan koordinat bayangan dari segitiga tersebut!
Transformasi geometri adalah bagian penting dalam Matematika yang sering digunakan dalam berbagai situasi kehidupan nyata, mulai dari pencerminan bayangan di cermin hingga perubahan ukuran dalam gambar. Dengan memahami konsep translasi, refleksi, rotasi, dan dilatasi, kamu bisa lebih mudah menyelesaikan soal-soal Matematika yang berkaitan dengan transformasi ini.
Contoh Soal Transformasi Geometri dengan Grafik
Agar pemahaman tentang transformasi geometri semakin kuat, mari kita lihat contoh soal lengkap dengan grafik yang menunjukkan perubahan posisi objek pada bidang Cartesius.
Contoh 1: Translasi
Misalkan titik P(2, 3) ditranslasikan sejauh 4 satuan ke kanan dan 2 satuan ke atas. Tentukan koordinat akhir dari titik P dan gambarkan posisi sebelum dan sesudah translasi.
Pembahasan:
Koordinat awal P adalah (2, 3). Setelah translasi dengan perpindahan 4 satuan ke kanan dan 2 satuan ke atas, kita dapat menggunakan rumus translasi:
P’(x’, y’) = P(x + a, y + b)
Dengan a = 4 dan b = 2, maka:
P’(2 + 4, 3 + 2) = P’(6, 5)
Jadi, koordinat akhir dari titik P adalah (6, 5).
Berikut adalah grafik translasi titik P:
Contoh 2: Refleksi
Titik A(-3, 4) direfleksikan terhadap sumbu-x. Tentukan koordinat bayangan titik A dan gambarkan perubahan posisi titik tersebut.
Pembahasan:
Koordinat awal A adalah (-3, 4). Saat titik direfleksikan terhadap sumbu-x, koordinat y akan menjadi negatif, sementara koordinat x tetap. Rumus refleksi terhadap sumbu-x adalah:
P’(x’, y’) = P(x, -y)
Dengan koordinat awal A(-3, 4), maka:
A’(-3, -4)
Jadi, bayangan titik A setelah direfleksikan terhadap sumbu-x adalah A’(-3, -4).
Berikut adalah grafik refleksi titik A:
Contoh 3: Rotasi
Titik B(2, 3) dirotasi sejauh 90° berlawanan dengan arah jarum jam terhadap titik pusat (0,0). Tentukan koordinat bayangan titik B dan gambarkan hasil rotasinya.
Pembahasan:
Koordinat awal B adalah (2, 3). Jika titik ini dirotasi 90° berlawanan arah jarum jam, kita menggunakan rumus rotasi berikut:
P’(x’, y’) = (-y, x)
Dengan koordinat B(2, 3), maka hasil rotasi adalah:
B’(-3, 2)
Jadi, koordinat bayangan titik B setelah rotasi 90° berlawanan arah jarum jam adalah B’(-3, 2).
Berikut adalah grafik rotasi titik B:
Contoh 4: Dilatasi
Sebuah segitiga ABC dengan koordinat A(1, 2), B(3, 4), dan C(5, 6) didilatasi terhadap titik pusat (0, 0) dengan faktor pengali 2. Tentukan koordinat bayangan dari segitiga tersebut dan gambarkan hasil dilatasinya.
Pembahasan:
Jika faktor pengali dilatasi adalah 2, maka setiap titik diperbesar dua kali lipat dari titik pusat (0, 0). Rumus dilatasi adalah:
P’(x’, y’) = (k * x, k * y)
- Untuk titik A(1, 2): A’(2 * 1, 2 * 2) = A’(2, 4)
- Untuk titik B(3, 4): B’(2 * 3, 2 * 4) = B’(6, 8)
- Untuk titik C(5, 6): C’(2 * 5, 2 * 6) = C’(10, 12)
Jadi, bayangan segitiga ABC setelah didilatasi dengan faktor pengali 2 adalah A’(2, 4), B’(6, 8), dan C’(10, 12).
Berikut adalah grafik dilatasi segitiga ABC:
Dengan grafik dan contoh soal ini, kamu dapat lebih memahami cara kerja transformasi geometri, mulai dari translasi, refleksi, rotasi, hingga dilatasi. Menggunakan grafik sangat membantu untuk memvisualisasikan hasil dari setiap jenis transformasi, sehingga lebih mudah untuk memahami perubahan posisi dan ukuran objek.
Jangan lupa untuk selalu mempraktikkan berbagai soal dan memahami setiap langkah dalam proses transformasi. Semoga artikel ini membantu kamu memahami materi transformasi geometri dengan lebih baik. Selamat belajar dan terus berlatih!







